In this blog, my second on diamonds, I’ll discuss the physical and chemical properties of a diamond, then its optical properties in relation to its crystal structure and chemistry, and then their formation and associated geology.
CRYSTAL STRUCTURE AND PROPERTIES OF DIAMOND
To understand the physical properties of the diamond it’s important to understand its crystal structure, which underlies its strength, and its other mechanical properties. To understand the sources of the various colors observed in diamonds, it’s necessary to relate them to localized defects in the periodic array of carbon atoms within the crystal lattice, as well as to the impurity atoms in the lattice.
Physical Properties of Diamonds
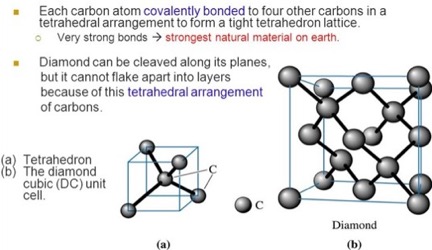
In this section those physical properties affecting diamond as a gemstone are described. Diamond, unique among minerals, is comprised of only one element, carbon. In the crystal lattice of diamond, the carbon atoms can be pictured as being located at each of the four corners of a tetrahedron, embedded in a cube, as seen in Slide 7 of [Ref 1] and shown in Figure 1.
in a Diamond.
Extension of the arrangement of the four carbon atoms in the tetrahedron to the lattice, results in the arrangement of carbon atoms in the cubic unit cell of the crystal lattice, as also shown in Figure 1. Bonds between the carbon atoms extend throughout the diamond crystal, as shown in Figure 3. Their strength and arrangement underlie the physical properties of the diamond.
Strength of a Diamond
With a hardness of 10 on the Mohs Hardness Scale [Ref 2], and a relative hardness scale of minerals in the range of 1-10, diamond is ranked as the hardest of minerals. The scale is approximately logarithmic. As a quantitative example, the tensile strength, or resistance to pulling, by natural diamonds has been measured within the range 2.8 – 2.93 GPa (452,776-473797 psi) [Ref 3]. In parallel, these large values of tensile strength are exceeded by values of the compressive strength of diamond, in the range 10-20 GPa (1,617,057-3,234,114 psi) [Ref 3]. This large compressive strength underlies the uses of diamond windows in the diamond anvil cell, as shown in Figure 2. Used for exerting very large pressures on a material for study of its properties [Ref 4]. Recently the formation of metallic hydrogen, by breakdown of molecular hydrogen, (under familiar conditions, a gas), at a pressure of 495 GPa (71.700,000 psi) was achieved using anvils of a specially treated synthetic diamond [Ref 5]. Interestingly, this result supports the hypothesis that the core of the planet Jupiter may be comprised of liquid metallic hydrogen [Ref 6].
The large strength values derive, in part, from the strength of the carbon-carbon bond in the diamond, having the energy of 346 (kilojoules)/(mole of carbon), [Ref 7], and from the pattern of orientation of carbon-carbon bonds within the lattice, with the exception of the pattern of those bonds crossing the octahedral planes of a crystal, along which the crystal can be cleaved. As seen below.

Cleavage in a Diamond
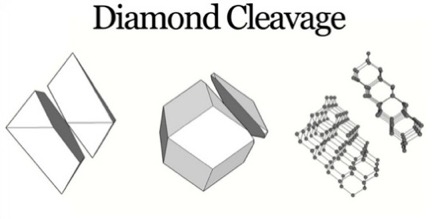
Despite the strength of the carbon bonds in the diamond, its lattice does possess a specific set of planes of weakness along which the severing of the bonds requires the least energy. In all other directions, with the application of shear force, the diamond lattice will resist compression or tension. Diamonds exhibit a perfect and easy cleavage or separation along planes parallel to any one of the eight faces of an octahedron, as can be seen in Figure 3 [Ref 8]. In any other direction the number of bonds necessary to be broken for cleavage are larger than along this octahedral plane. This feature underlies the use of intentional cleavage of a rough diamond in removing material prior to further steps in preparing a gem [Ref 9].
Visualizing cleavage in diamond
In Figure 4, a partial cleavage is seen to be exactly oriented, parallel to the opposing octahedral face [Ref 10]. Additionally, the view of the diamond lattice parallel to an octahedral plane and the slightly tilted view in Figure 3, shows that the minimum possible number of carbon-carbon bonds per unit area cross this plane, thus, requiring the least possible energy for cleavage.

As a caveat, because of its easy and perfect cleavage, and despite its hardness, toughness or tenacity, the ability to resist fracture is only fair to good, because its easy cleavage renders it susceptible to breaking.
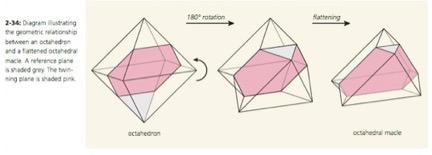
Twinning in Diamonds
Twinned crystals of diamond present a unique form, quite unlike that of a single crystal. Conceptually, twinning in diamonds occurs between the octahedral faces of two crystals, as shown diagrammatically in Figure 5 [Ref 11]. This twin form is also known as a macle. The reentrant angle at the base of the triangular faces of the macle is shown on the twin in Figure 6. Two macles can pair as shown in Figure 7, to form a Star-of-David twin [Ref 12].


Optical Properties of Diamond
The appreciation of diamonds as gemstones, lies in their sparkling brilliance, and in their colors, which span the rainbow. Their brilliance is due to their large refractive index and dispersion of colors. Their colors are due to the presence of impurities and defects in their crystal lattice.
Refractive index and dispersion
The refractive index of a gemstone is a measure of the magnitude of the angle at which light is bent, (refracted), as it enters from the outside [Ref 13]. If the refractive index of the material at which the light enters exceeds that at the exterior, the light will bend more towards the perpendicular (Figure 1 in Ref 13).
The brilliant appearance of a diamond, compared to other gemstones, stems from its larger refractive index and degree of dependence on the wavelength of the incident light. The brilliance, or dance of colors seen on a cut diamond stems from its large dispersion, which is a measure of splitting light into its constituent colors after entering the gemstone [Ref 14]. Such dispersion can be demonstrated by the rainbow of colors which exit from a glass prism, as shown in Figure 13. As a uniform measure for all gems, the dispersion is calculated as the difference in refractive index values measured with light at 430.8 in the violet and nm ad 686.7 nm in the red region [Ref 14]. The difference of the two values gives the dispersion of the diamond d = 2.451-2.407 = 0.044 [Ref 14]. This value is very large compared to other gemstones. For example, this value far exceeds the value of 0.014 for difference in the refractive index of light determined at two wavelengths, 430.8 nm in aquamarine (and also for emerald, heliodor, and morganite), the value of 0.018 for corundum (and also for ruby and sapphire) [Ref 15].

The angle at which visible light is bent as it enters the diamond depends directly on the wavelength-dependent refractive index. The cut of the gem, or the overall placement of the facets on the rear, sides and face, is designed to optimize the play of colors developed within the gem by dispersion for the viewer. The facets must be placed at angles calculated to optimally reflect the light back into the gemstone and position it to escape from the face of the gemstone. The American Standard Brilliant Cut [Ref 16], among others, maximizes the total amount of light and the play of its colors, leaving the gem as shown in Figures 14 and 15.


Impurities, Crystal Lattice Defects, and Color of Diamonds
Many of the structural impurities, which are sources of colors in diamonds, are described in the Shigley Chart [Ref 18]. In the list of color sources, nitrogen atoms are labeled N, as impurities substituting for carbon atoms in the diamond lattice, alone or associated with an adjacent lattice vacancy labeled V, and are seen to cause many of the colors which range over the green to red portion of the visible spectrum. Additionally, boron atoms, labeled B, as impurities substituting for carbon atoms, impart a blue color, while a single lattice vacancy labeled V, imparts a green color. Groups of vacancies can impart a yellowish-brown color. Also, interstitial hydrogen atoms lying in spaces between carbon atoms, impart a yellowish-brown color. In another study, an interstitial nickel atom as an impurity, (with an associated large-sized split-vacancy Ni-2V), was found to impart a green color [Ref 19].
The Formation of Diamonds [Ref 20]
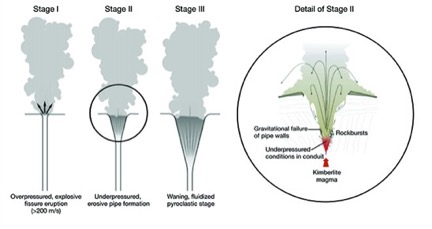
Diamonds are formed within the earth’s mantle at remarkable depths of 80 kilometers and greater, and at notable pressures of 2.6 Gigapascals or 377098 psi and greater, as shown in Figure 22. They are violently projected to the surface by magma rising at velocities of 200 meters per second, which fractures the overhead rock and forms a crater at the surface containing a plug of the host rocks of diamonds, as shown in Figure 23. The major host rocks are kimberlite [Ref 21] or lamproite [Ref 22] as shown in Figures 23 and 24. Both rocks are breccias formed of cemented fragments, which resulted from the rock fracturing. Figure 27, taken of the Diavik mine in Canada, shows the circular contours of two kimberlite ore bodies on the surface [Ref 20].

[Ref 21].

[Ref 22].

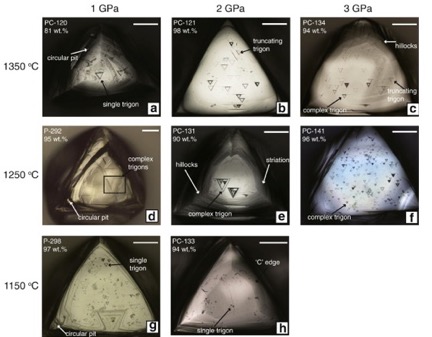
Resorption with etching and rounding of the surfaces of diamonds can occur due chemical attack by the acidic environment, due to the presence water (H2O), and oxidation of the diamonds carbon to form carbon dioxide (CO2) within the melt of the magma [Ref 23]. Examples of the rounding of the shapes of octahedral and cubic crystals with increasing resorption are shown in Figure 28.